3 functions to perform linear regression in Python
By Jia Liu in python regression statistics
December 12, 2021
So why are we here?
Recently I helped another PhD student in our department to solve a problem in her python script that performs linear regression. In this script, two linear regression models based on the input data were generated using two methods (LinearRegression() from sklearn.linear_model; the OLS function from statsmodels.api). The
R-square as well as
Adjusted R-Square calculated from these two models were very different. That inspired me to start this post: while there are always different methods that performs the same process, disagreement among the results generated from different methods can be a headache. Here we will go through three widely used methods that build linear regression models in python: sklearn, statsmodel.api, and statsmodels.formula.api using a randomly generated dataset, and see how we can avoid the problem.
Generate a Random dataset
We will first import packages that needed, and then generate a random dataset:
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import statsmodels.api as sm
# Generate 'random' data
np.random.seed(0)
X = 2.5 * np.random.randn(150) + 1 # Array of 150 values with mean = 1, stddev = 2.5
res = 0.5 * np.random.randn(150) # Generate 150 residual/random error terms
y = 4 + 0.3 * X + res # Get the actual values of Y assuming y_i = 4 + 0.3x_i + e_i
# Create pandas dataframe to store our X and y values
df = pd.DataFrame(
{'X': X,
'y': y}
)
df.head()
## X y
## 0 5.410131 5.588918
## 1 2.000393 5.456789
## 2 3.446845 4.661676
## 3 6.602233 5.567451
## 4 5.668895 5.651442
Let’s visualize the regression:
sns.set_theme(color_codes=True)
sns.regplot(x="X", y="y", data = df).set(title = "y vs X")
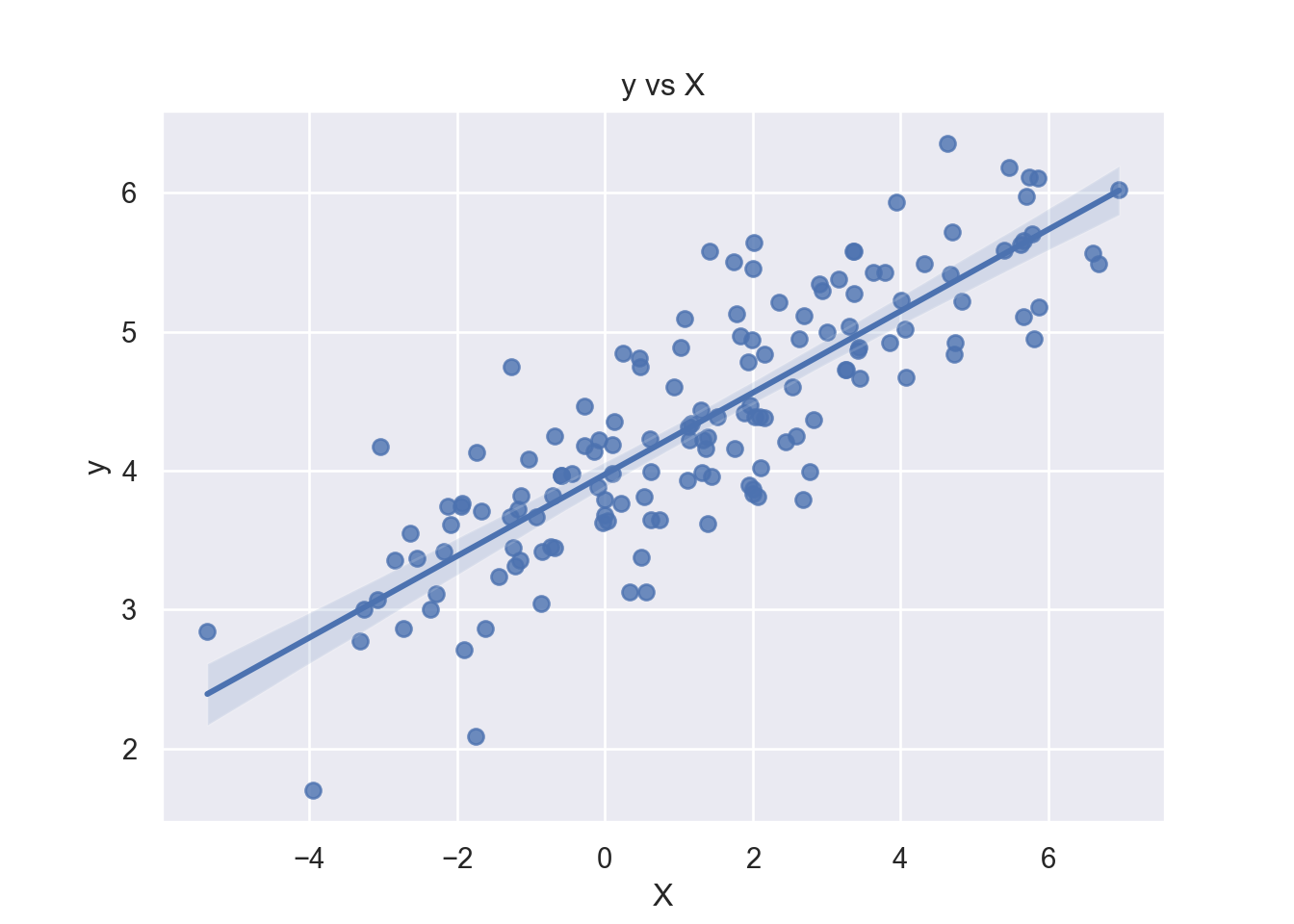
There seems to be a positive trend between \(y\) and \(X\), but there’s also a certain extent of dispersion of data points from the predicted regression line as shown in the figure.
Linear regression
Since our goal here is to show how to apply linear regression using three methods in python, but not analyze any data, we will simply build the models based on the simulated data, make predictions using the predictor \(X\) in the simulated data, and get the summaries.
Use Sklearn
Build and fit the model:
from sklearn.linear_model import LinearRegression
model_sk = LinearRegression()
model_sk.fit(df[['X']], df['y'])
## LinearRegression()
print(f'The coefficient of `model_sk` is {model_sk.coef_[0]}')
## The coefficient of `model_sk` is 0.2935352606493269
print(f'The intercept of `model_sk` is {model_sk.intercept_}')
## The intercept of `model_sk` is 3.9733289338377187
Get the R square:
# Calculate R square
R2 = model_sk.score(df[['X']], df['y'])
print(f'The R square of `model_sk` is {R2}')
## The R square of `model_sk` is 0.7042485663051222
There seems to be no built-in function for adjusted R square in LinearRegression of sklearn. As we know $$R_{adj}^2 = 1 - \frac{(1-R^2)(n-1)}{n-k-1}$$ where \(n\): the number of subjects in the sample; \(k\): the number of variables, we can manually calculate the adjusted R square:
# Calculate adjusted R square
#R2 = model_sk.score(df[['X']], df['y'])
n = len(X)
p = 1
adj_R2 = 1-(1-R2)*(n-1)/(n-p-1)
print(f'The adjusted R square of `model_sk` is {adj_R2}')
## The adjusted R square of `model_sk` is 0.7022502458071839
Use statsmodel.api
statsmodels.api.OLS can be used for ordinary least squares model. One thing to notice as mentioned in the
Statsmodels API is: …An intercept is not included by default and should be added by the user. See statsmodels.tools.add_constant()…. Including intercept or not can make a drastic difference on the model. Let’s have a look.
- Default: Without intercept
Model summary:
import statsmodels.api as sm
model_statsm = sm.OLS(y, X)
results_1 = model_statsm.fit()
print(results_1.summary())
## OLS Regression Results
## =======================================================================================
## Dep. Variable: y R-squared (uncentered): 0.358
## Model: OLS Adj. R-squared (uncentered): 0.353
## Method: Least Squares F-statistic: 83.00
## Date: Tue, 14 Dec 2021 Prob (F-statistic): 5.09e-16
## Time: 15:20:58 Log-Likelihood: -403.54
## No. Observations: 150 AIC: 809.1
## Df Residuals: 149 BIC: 812.1
## Df Model: 1
## Covariance Type: nonrobust
## ==============================================================================
## coef std err t P>|t| [0.025 0.975]
## ------------------------------------------------------------------------------
## x1 0.9276 0.102 9.110 0.000 0.726 1.129
## ==============================================================================
## Omnibus: 0.930 Durbin-Watson: 0.418
## Prob(Omnibus): 0.628 Jarque-Bera (JB): 0.943
## Skew: -0.037 Prob(JB): 0.624
## Kurtosis: 2.619 Cond. No. 1.00
## ==============================================================================
##
## Notes:
## [1] R² is computed without centering (uncentered) since the model does not contain a constant.
## [2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Parameters:
results_1.params
## array([0.92757837])
- Add an intercept
Model summary:
import statsmodels.api as sm
X_cons = sm.add_constant(X)
model_statsm = sm.OLS(y, X_cons)
results_2 = model_statsm.fit()
print(results_2.summary())
## OLS Regression Results
## ==============================================================================
## Dep. Variable: y R-squared: 0.704
## Model: OLS Adj. R-squared: 0.702
## Method: Least Squares F-statistic: 352.4
## Date: Tue, 14 Dec 2021 Prob (F-statistic): 5.49e-41
## Time: 15:21:00 Log-Likelihood: -104.36
## No. Observations: 150 AIC: 212.7
## Df Residuals: 148 BIC: 218.7
## Df Model: 1
## Covariance Type: nonrobust
## ==============================================================================
## coef std err t P>|t| [0.025 0.975]
## ------------------------------------------------------------------------------
## const 3.9733 0.045 88.572 0.000 3.885 4.062
## x1 0.2935 0.016 18.773 0.000 0.263 0.324
## ==============================================================================
## Omnibus: 0.109 Durbin-Watson: 2.235
## Prob(Omnibus): 0.947 Jarque-Bera (JB): 0.121
## Skew: 0.061 Prob(JB): 0.941
## Kurtosis: 2.933 Cond. No. 3.32
## ==============================================================================
##
## Notes:
## [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Parameters:
results_2.params
## array([3.97332893, 0.29353526])
-
Summary:
-
In our simulated data, we assumed there is an intercept. Thus the default model of
statsmodel.apithat assumes no intercept didn’t fit the data very well. -
Coefficients generated from the model with intercept are similar to the ones used to simulate the data; R-square and adjusted R square are close to the ones from
sklearnmodel -
We can include an intercept to a
statsmodel.apimodel by usingsm.add_constant()function to add a constant variable to\(X\)as in the example above.
-
Use Statsmodels formula
statsmodels.formula.api allows users to define the regression model using a R-like formula.
- Default: With intercept
Note that unlike statsmodel.api, the default ols model made by statsmodels.formula.api includes an intercept:
from statsmodels.formula.api import ols
formula = 'y ~ X'
model_sfa = ols(formula = formula, data = df).fit()
model_sfa.summary()
| Dep. Variable: | y | R-squared: | 0.704 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.702 |
| Method: | Least Squares | F-statistic: | 352.4 |
| Date: | Tue, 14 Dec 2021 | Prob (F-statistic): | 5.49e-41 |
| Time: | 15:21:02 | Log-Likelihood: | -104.36 |
| No. Observations: | 150 | AIC: | 212.7 |
| Df Residuals: | 148 | BIC: | 218.7 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 3.9733 | 0.045 | 88.572 | 0.000 | 3.885 | 4.062 |
| X | 0.2935 | 0.016 | 18.773 | 0.000 | 0.263 | 0.324 |
| Omnibus: | 0.109 | Durbin-Watson: | 2.235 |
|---|---|---|---|
| Prob(Omnibus): | 0.947 | Jarque-Bera (JB): | 0.121 |
| Skew: | 0.061 | Prob(JB): | 0.941 |
| Kurtosis: | 2.933 | Cond. No. | 3.32 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Parameters predicted from the above model are close to the coefficients we used to simulate the data. The R square and adjusted R-square also agree with the previous sklearn and statsmodel.api (with intercept) methods. Great!
- Exclude the intercept
To build a model without an intercept using statsmodels.formula.api (data may already been mean-centered), we can define the formula as \(formula = \text{'}y \sim X - 1\text{'}\) (-1 will exclude the intercept):
from statsmodels.formula.api import ols
formula = 'y ~ X-1'
model_sfa = ols(formula = formula, data = df).fit()
model_sfa.summary()
| Dep. Variable: | y | R-squared (uncentered): | 0.358 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.353 |
| Method: | Least Squares | F-statistic: | 83.00 |
| Date: | Tue, 14 Dec 2021 | Prob (F-statistic): | 5.09e-16 |
| Time: | 15:21:03 | Log-Likelihood: | -403.54 |
| No. Observations: | 150 | AIC: | 809.1 |
| Df Residuals: | 149 | BIC: | 812.1 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| X | 0.9276 | 0.102 | 9.110 | 0.000 | 0.726 | 1.129 |
| Omnibus: | 0.930 | Durbin-Watson: | 0.418 |
|---|---|---|---|
| Prob(Omnibus): | 0.628 | Jarque-Bera (JB): | 0.943 |
| Skew: | -0.037 | Prob(JB): | 0.624 |
| Kurtosis: | 2.619 | Cond. No. | 1.00 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
- Posted on:
- December 12, 2021
- Length:
- 7 minute read, 1313 words
- Categories:
- python regression statistics
- See Also: